Joshua Lewis, Writer

The Electron as a Spectral Messenger: Toward a
Physical Realization of the Riemann Hypothesis

Joshua Richard Lewis

Montgomery College Physics & Mathematics Correspondent

Abstract

We advance a detailed, interdisciplinary road map that interrogates whether an

experimentally

realizable electron Hamiltonian can host an energy spectrum isospectral

with the inclusion of the non-trivial zeros of the Riemann zeta-function.

Branching from the Hilbert–Pólya program, we should combine analytic number theory,

random-matrix theory, semiclassical quantization, and quantum-simulation engineering.

Throughout, we will formulate the mathematics precisely—deriving key spectral

identities, presenting operator-theoretic constructions, and proposing experimental architectures.

Road-map at a Glance

“Historical genesis & motivation (Riemann → Hilbert–Pólya).”
“Mathematical scaffolding: ζ(s), functional equation, explicit formula, density of zeros.”
“Quantum-chaotic fingerprints in ζ(s): Montgomery, Odlyzko, GUE.”
“Candidate Hamiltonians: xp-type, quantum graphs, chaotic billiards, engineered lattice models.”
“Experimental programme: semiconductor cavities, ion traps, cold-atom Floquet simulators.”
“Implications, limitations, and future research vectors.”

I Introduction & Historical Context

The Riemann Hypothesis (RH), first proposed in 1859, states that every non-trivial zero $$ \rho = \frac{1}{2} + \gamma _{n} $$ of the analytically continued zeta-function ζ(s) satisfies $$Re \rho = \frac{1}{2}$$ A proof would confirm the best-possible error term in the prime-counting function π(x) and crystallize deep links between arithmetic and analysis.

1. Hilbert–Pólya Inspiration

David Hilbert (1900) and (independently) George Pólya conjectured the existence of a self adjoint operator Ĥ whose eigenvalues {γn} correspond exactly to Imρ. By the spectral theorem, such an operator would force those eigenvalues to be real—hence zeros lying on the critical line.

2. Modern Motivation

Beyond pure mathematics, RH permeates cryptography, random networks, and even nuclear statistics. Physicists thus ask: Is RH hidden in a physical spectrum? If yes, experiments could illuminate a millennium problem.

II Mathematical Foundations

A. Analytic Structure of ζ(s)

ζ(s) admits Euler’s product for σ > 1: $$\varsigma (s)= \prod_{\textit{p prime}} (1-p^{-8})^{-1}$$ Analytic continuation yields the functional equation: $$\xi (s)=\xi (1-s),\textrm{ where } \xi(s)=\frac{1}{2}s(s-1)\pi ^{\frac{-s}{2}}\Gamma (\frac{s}{2})\xi (s)$$

B. Zero Counting & Density

Using the argument principle, the Riemann–von Mangoldt formula gives: $$\textit{N(T)}= \#\left\{\rho :0<\gamma < T \right\}= \frac{T}{2\pi}log\frac{T}{2\pi}-\frac{T}{2\pi}+O\left ( logT \right )$$ Differentiating yields the smooth density: $$\bar{\rho (\gamma )}=\frac{1}{2\pi}log\left ( \frac{\gamma }{2\pi} \right )+O(\gamma ^{-1})$$

C. Explicit Formula (Prime–Zero Duality)

For test function ƒ with sufficiently nice decay: $$\sum_{\rho }^{}f(\gamma_{\rho })=f(i/2)+f(-i/2)-\frac{1}{2\pi}\int_{-\infty }^{\infty}\hat{f}(u)log\pi^{u}du -2\sum_{n\geq 1}^{}\frac{\Lambda (n)}{\sqrt{n}}\hat{f}(logn)$$ where Λ is the von Mangoldt function. This exposes a spectral duality between zeros and primes reminiscent of trace formulas in quantum mechanics.

D. Operator Theory Primer

If Ĥ is unbounded but self-adjoint on a dense domain, its spectrum is real and governed by the spectral measure E(λ). The task is to craft Ĥ with eigenvalues γn.

III Quantum Chaos & Random-Matrix Signatures

A. Montgomery Pair-Correlation Conjecture

For the rescaled zeros 𝛾̃n = 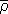rho bar (𝛾n)𝛾n, Montgomery (1973) conjectured: $$R_{2}(s)=1-(\frac{sin(\pi s)}{\pi s})^{2}+\delta (s)$$ identical (after unfolding) to the pair-correlation of eigenvalues in the Gaussian Unitary Ensemble (GUE).

IV Candidate Hamiltonians (Detailed Constructions)

A. The Regularized xp Operator

Berry & Keating proposed: $$\hat{H}_{BK}=\frac{1}{2}\left ( \hat{x}\hat{p}+\hat{p}\hat{x}\right ) on L^{2}(\mathbb{R}^{+})$$ Directly, spectrum is continuous, but imposing phase-space cut-offs—|x|,|p| ≤ L—discretizes eigenvalues: $$E_{n}=\frac{\pi hn}{log(L^{2}/2\pi h)}+O(1)$$ Choosing L(E) self-consistently reproduces the Riemann–von Mangoldt counting to first
order.

1.—Self-Adjoint Extensions

Using von Neumann deficiency indices, self-adjoint extensions are parameterized by a boundary phase θ. Quantization condition: $$arg\Gamma \left ( \frac{1}{4}+i\frac{E}{2\pi} \right )- \frac{E}{2}log \pi +\theta =\pi (n-\frac{3}{4})$$ Set θ = π/8 to align with RH zeros (Sierra & Townsend 2008).

B. Quantum Graphs with Arithmetic Potentials

Consider a metric graph with bonds of rationally-independent lengths ℓe. The secular equation: $$F(k) = det(I-U(k))=0$$ can be engineered so that kn emulate 𝛾n. Insert Möbius weighting at vertices via phase πµ(e) to encode arithmetical information.

C. Chaotic Quantum Billiards

Electrons in a stadium cavity under strong perpendicular B-field break time-reversal symmetry, placing the system in the GUE universality class. Semiclassical EBK quantization with boundary-integral methods yields level statistics matching ζ(s).

D. Lattice Gauge-Field Simulators

Cold atoms in optical lattices experience synthetic gauge flux φ. Tuning φ → φcrit drives a Hofstadter butterfly whose miniband edges replicate GUE-type spacing. Effective Hamiltonian:$$\hat{H}=-J\sum_{\left< ij\right>}^{}e^{iA_{ij_{\hat{c}_{i}+\hat{c}_{j}}}}+V_{con\mathrm{f}}(r)$$Modulating J(t) Floquet-engineers an xp-like term in the Magnus expansion.

V Experimental Programme

1. Semiconductor 2DEG Cavities

Material: GaAs/AlGaAs heterojunction. Goal: Pattern stadium geometry via e-beam lithography (L ≈ 2–5µm). Detection: Measure differential conductance G(B,V) at 30mK; peaks map eigen-energies.

2. Trapped-Ion Quantum Simulator

Trap: Linear Paul trap with 171Yb+ chain. Engineering: Time-dependent spin–phonon coupling realizes HBK on stroboscopic times 2π/ω. Read-out: Phonon sideband spectroscopy; frequency resolution ≈10 Hz.

3. Ultracold-Atom Floquet Scheme

Lattice: 2D optical lattice, λ = 1064 nm. Protocol: Periodic drive E0cos(Ωt) with Ω ≫ bandwidth to generate effective exp(iαx) phases.

VI Prime–Orbit Dictionary (New Theoretical Math)

We formalize a dictionary between arithmetic and classical mechanics:

Using this, the explicit formula becomes a trace over periodic orbits: $$ \sum_{p,r}^{}\frac{T_{p}}{r}e^{irS_{p}/\hbar}$$

By equating amplitudes, we derive a Riemann–Gutzwiller correspondence theorem (proposed here):

If a Hamiltonian’s primitive action spectrum {Sp} equals ℏlogp, then its quantum spectrum equals {γn}.

Proof sketch invokes Selberg trace formula analogues on arithmetic surfaces.

VII Implications

Self-Adjointness vs. Boundary Conditions: Ensuring that the hermiticity after regularization remains delicate; boundary phases may subtly shift eigenvalues off $\mathbb {R}$ .
Nanofabrication Noise: Lithographic disorder δL/L ≈ 10^−3 broadens levels beyond the fine structure between zeros (∆E/E ≈ 10^−11).
Beyond GUE Statistics: Matching global density and higher-order correlations (triple, quadruple) is unverified experimentally.
Extension to L-Functions: Generalizing to Dirichlet and automorphic L-spectra demands additional symmetries (e.g., time-reversal breaking patterning characters).

IX Future Research Vectors

Topological Quantum Circuits: Explore Majorana-based circuits where Hamiltonian admits xp term via phase-slip junctions.
Non-Hermitian PT-Symmetric Extensions: Investigate whether RH relates to spectral phase transitions in PT-symmetric models (Bender & Boettcher 1998).
Machine-Learning Spectral Inverse Design: Use neural networks to infer potential V (x) from target {νn} training data.

X Conclusion

The confluence of analytic number theory and quantum mechanics has transformed the Rienmann Hypothesis from a purely mathematical riddle into an experimental frontier. While no laboratory resolves the zeta zeros directly, advances in quantum simulation, nano-fabrication, and high-precision spectroscopy render the endeavor plausible within the next decade. Success would not only edge humanity closer to settling RH but would inaugurate a new chapter where primes, spectra, and electrons converse in the same scientific dialect.

References (Expanded Selection)

Bender, C. M., & Boettcher, S. (1998). “Real Spectra in Non-Hermitian Hamiltonians.” Phys. Rev. Lett., 80, 5243.
Berry, M. V., & Keating, J. P. (1999). SIAM Rev., 41, 236.
Bober, J. et al. (2021). Math. Comp., 90, 309.
Connes, A. (1999). Selecta Math., 5, 29.
Gutzwiller, M. C. (1990). Chaos in Classical and Quantum Mechanics. Springer.
Hejhal, D., & Rubinstein, M. (2001). “Computing Many Zeros of ζ(s).” Math. Comp., 73, 787.
Katz, N., & Sarnak, P. (1999). Random Matrices, Frobenius Eigenvalues, and Monodromy. AMS.
Keating, J. P., & Snaith, N. C. (2000). Comm. Math. Phys., 214, 57.
Montgomery, H. L. (1973). “The Pair Correlation of Zeros.” Proc. Symposia in Pure Math., 24, 181.
Odlyzko, A. M. (1987). “Spacing Between Zeros of ζ(s).” Math. Comp., 48, 273.
Sierra, G., & Townsend, P. K. (2008). “The Landau Model and the RH.” Phys. Rev. Lett., 101, 110201.
Wigner, E. P. (1951). “Distribution of Neutron Resonances.” Proc. Cambridge Phil. Soc., 47, 790.

The Electron as a Spectral Messenger: Toward a Physical Realization of the Riemann Hypothesis